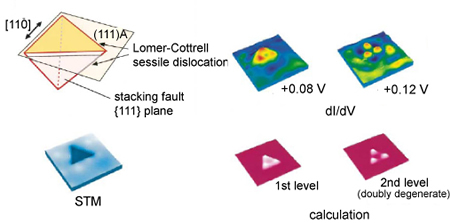
半導体量子ドット 2次元電子系といえば半導体に形成される 2次元電子系がよく知られています。例えば,Si-MOS や GaAs/AlGaAs ヘテロ構造界面に形成される三角ポテンシャルに閉じ込められた電子は量子化によってz軸方向の自由度が失われ 2次元系として振舞います。これはグラファイト表面に物理吸着した単原子層3Heが低温で 2次元フェルミ系を形成するのと似ています(注)。そこで我々は半導体表面に形成される 2次元電子系や表面に正三角形の欠陥として現れる 0次元電子系(いわゆる量子ドット)の電子状態を ULT-STM を用いて実空間観測することも目的としています。 従来の低次元電子系の研究の多くは伝導度の測定に限られてきましたが,近年走査トンネル分光法(STS)を使った電子状態の空間分布の観測が可能になってきました。下図は分子線エピタキシャル(MBE)法で GaAs(111)A 上に成長させた InAs 薄膜の表面反転層に形成されるた 2次元電子系が,薄膜成長過程で形成される四面体積層欠陥(表面では正三角形の欠陥として現れる)の内部に閉じ込められることで実現する擬 0次元電子系(量子ドット)の低温・ゼロ磁場下で STM/STS 観測した例です(下図:NTT 基礎研平山グループ)。ここでは量子ドットの基底状態と第1励起状態の電子密度の分布が観測され計算結果とよく一致することが分かります。
我々の研究室では NTT 基礎研の平山グループとの共同研究で ULT-STM/STS を使った 2次元および,0次元電子系の超低温・高磁場中 STS 測定を行っています。2次元電子系では先に説明した量子ホール効果による端状態が直接観測できる様子を実空間観測できる可能性がありますし,0次元電子系では磁場を印加することで上図のような量子化された準位の軌道縮退が解けることなどが期待されます。 (注):ただし,3He と電子では零点振動エネルギーの距離(r)依存性は r-2 であるのに対し,粒子間相互作用のr依存性は 3He が r-12(近距離斥力),電子が r-1(遠距離斥力)と異なるので,相互作用/零点振動エネルギーの比は 3He の場合 r が小さいほど大きく,電子の場合r が大きいほど大きいという興味深い差異があります。 [1] Kanisawa et al., Phys. Rev. Lett. 87, 196804 (2001). |