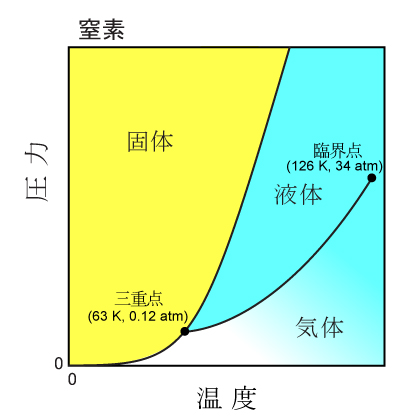
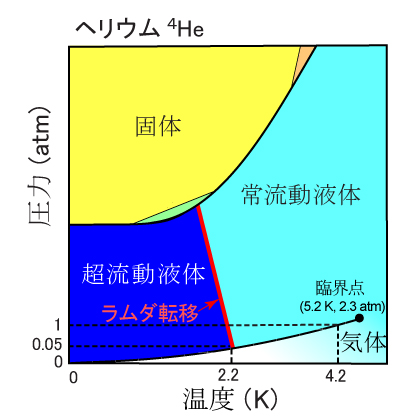
超流動ヘリウムの不思議 ヘリウム4の状態相図 一般に,原子同士や分子同士の間には引力的な相互作用が働きます。そのため,物質を冷却してゆくと気体から液体になり,最後は固体になります。このような物質の状態変化を「相転移」といいます。図1には,窒素分子(N2)の状態相図を示しました。熱擾乱の少ない低温では,引力エネルギーをできるだけ低くしようとして規則正しい結晶構造をとり,絶対零度で,原子や分子は各格子点で完全に静止すると予想されます。 そうした古典力学的な物質観は,20世紀初頭の量子力学の誕生とともに,大きな修正を求められました。ハイゼンベルクの不確定性原理によれば,粒子を狭い空間に閉じ込めると,温度に依らず「零点振動」とよばれる振動運動をします。零点振動の運動エネルギーは,粒子が軽いほど(質量に反比例して),また,閉じ込める空間が狭いほど(その2乗に反比例して)大きくなります。そのため,原子質量が水素に次いで小さいヘリウム(He)の場合,圧力をかけない状態では,絶対零度でさえ固化せず,液体状態にとどまります。その方が,零点振動の運動エネルギーが下がるからです。絶対零度でも安定して存在する液体を「量子液体」とよびます。その結果,図2に示したように,4Heの状態相図には三重点(気体,液体,固体が共存する相図上の1点)が存在しません。そのかわり,約2 K以下で,液体相は超流動相という興味深い状態に相転移します。
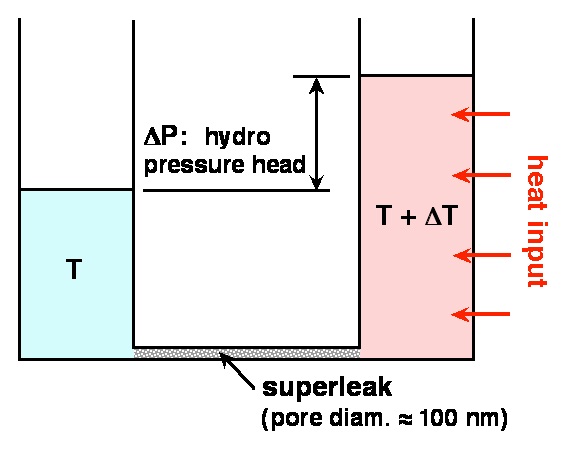
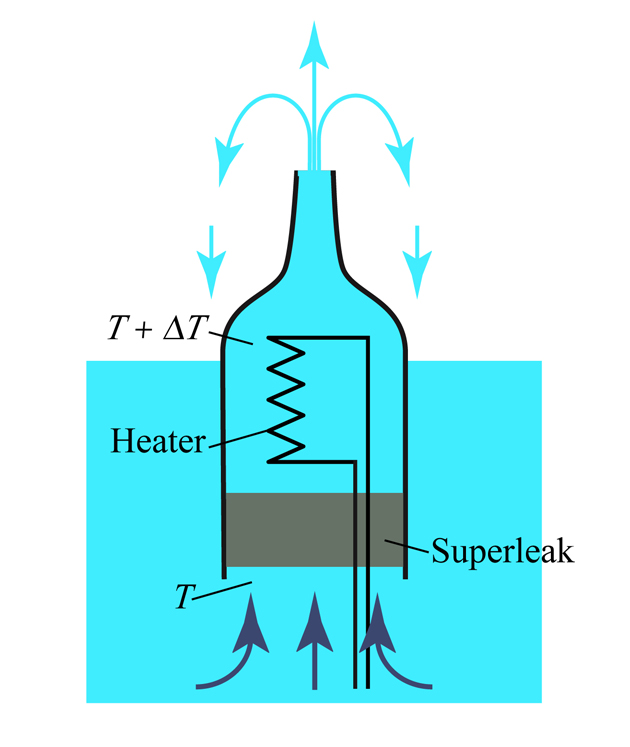
ラムダ転移 超流動状態では通常の液体では考えることのできない不思議な現象が沢山見られます。まずは,液体4Heが超流動転移する瞬間を動画1で見てください。 液体4Heの沸点は1気圧下で4.2 Kですが,その蒸気を真空ポンプで減圧して蒸発の潜熱を奪うと,蒸気圧曲線に沿って温度が下がります。最初は通常の液体のように液中のあちらこちらから沸騰する様子が見られます。ところが,2.17 Kに到達すると,沸騰がピタリと止むという劇的な変化を示します。これが超流動状態への相転移で,その温度を「ラムダ点」(Tλ = 2.17 K)とよびます。超流動相のことを「He-II」とよぶこともあります(これに対して,Tλより高温を「He-I」とよぶ)。 この沸騰の停止は,超流動状態の特徴である桁違いに大きい熱伝導度のために,液中で温度の不均一(揺らぎ)が生じなくなるために起きます。この状態では,原子は液面からだけ静かに蒸発します。激しく沸騰していた液体4Heが突然静かになり,液面が鏡面のようになる。この現象は肉眼でガラスデュワー(ガラスの断熱二重容器)越しに見ることができ,感動します。 スーパーリーク 超流動状態では,粘性が桁違いに小さいので,通常の液体ではとても通過できないような小さな穴でも通ることができます。ガラス管の底を黒板で使うチョークで隙間なく栓をして,ガラス管内に常流動状態の液体4Heを満たします。チョークの粉の粒径は,図3の走査型電子顕微鏡写真にあるように,1 μm(千分の1ミリメートル)以下と小さいので,粘性をもつ普通の液体がチョークをすり抜けて液が滴り落ちることは決してありません。 ところが,温度をラムダ点以下にすると,超流動4Heはチョークの中をすり抜けて下へポタポタと漏れ出てしまいます。その様子を下の動画2で見て下さい。このように,超流体のみを通過させる狭い隙間のことを「スーパーリーク」とよびます。チョークを通り抜ける流速は低温ほど大きくなりますが,その理由は,超流体にはそれを超えると粘性が発生してしまう流速(これを「臨界速度」とよぶ)(注1)があるのですが,臨界速度がラムダ点以下でゼロから低温になるほど徐々に大きくなるからです。 フィルムフロー フィルムフローとは,容器に汲んだ超流体が,勝手に容器の外に流れ出てしまう現象のことです。動画3を見てください。 じつは,直接,液体に触れていない容器壁の表面にも目に見えないほど薄い液体4Heの膜が吸着しており(厚みはおよそ10 nm程度),その薄膜を伝って超流体が内壁を這い上がり外壁を下降して,ついには容器の底から下に滴り落ちるのです。薄膜が吸着する理由は,ガラス表面とHe原子の間に,He原子同士の間より強い引力相互作用(ファン・デル・ワールス引力)が働くからです(注2)。毛細管現象と同じ原理です。ですから,どんな液体でも吸着薄膜は存在します。しかし,粘性が有限である限り,固体壁表面からわずか10 nmしか離れていない薄膜が流れることは不可能です。もちろん,動画3にあるように,常流動状態の液体4Heでもフィルムフローは起きません。ところが,薄膜が超流動状態になると臨界速度の範囲内で摩擦なく流動する,つまりフィルムフローが可能となります。動画の後半にあるように,外から白熱灯の光を当てると,薄膜の温度がTλより上がることでフィルムフローは瞬時に止まり,白熱灯を消すとまた始まります。 熱機械効果/噴水効果 超流動4Heを図4のようなスーパーリークでつないだ2つの容器に入れて,最初,液面を等しくしておきます。ここで,右側の容器の液温をヒーターでわずかに上げて左側と一定の温度差ΔTをつけると,右容器の液面が上昇して液面差が生じます。この現象を「熱機械効果」といい,液面差のため生じた静水圧の差ΔPはΔTに比例します(ラムダ点以下の温度までしか昇温しないのでT + ΔT < Tλ)。 どんな液体でも液温を上げればわずかに体積膨張しますが,それによる液面の上昇はほんの少しです。一方,熱機械効果は,わずか0.01 Kの昇温で数十cmもの液面差が生じます。液面が容器の上端を超えるほど熱を加えると,動画4のように超流体が上端から噴き出します。これが「噴水効果」です。この実験では,スーパーリークとしてグラファイトの微粉末を用いており(黒い部分),ガラス容器内が図4の右容器に相当し,容器外の液槽が左容器に相当します。外から入る光の輻射熱をグラファイトが選択的に吸収することで容器の内外の超流体に温度差をつけています。
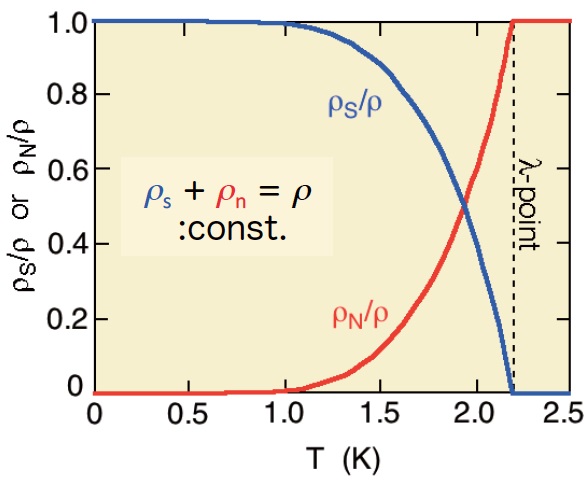
2流体モデル 熱機械効果や噴水効果は,超流体の重要な現象論である「2流体モデル」によってはじめて説明することができます。じつは,ラムダ点以下の超流体は,超流動成分と常流動成分の2成分が混ざり合った状態にあるかのように振る舞うのです。ただし,液体をいくらミクロに分割しても,両成分を空間的に分離することはできません。その意味では,超流体は完全に均質です。超流動成分はエントロピーをもたず,壁と摩擦なしに流れることができます。一方,常流動成分はラムダ点以上の液体と同じくエントロピーをもち,粘性ももっています。両者はそれぞれ独立に流れることができますが,その間には摩擦は生じません。超流動成分の密度をρS,常流動成分の密度をρNと書けば,両者の和ρ = ρS + ρN(通常の密度)は温度に依らず一定ですが,その比ρS/ρNは図6のように大きな温度依存性をもちます(注3)(注4)。例えば,ρS/ρは,ラムダ点でゼロから連続的に増加し,T → 0で100%に近づくので,熱力学第三法則の要請通り,絶対零度で全エントロピーもゼロとなります。 熱機械効果や噴水効果の実験では,2つの容器に温度差をつけたので,そのままでは化学ポテンシャルに差が生じてしまいます(高温側の化学ポテンシャルの方が低い)。そこで,それを打ち消すだけの圧力差をつけるべく超流動成分だけがスーパーリークを通じて低温の容器から高温の容器に流れ込むのです。生ずる圧力差ΔPと温度差ΔT には,次式の関係があります。 ΔP = ρSΔT ここでρとSは液体4Heの密度と単位質量あたりのエントロピーです。上述したように,エントロピーの担い手は常流動成分だけです。スーパーリークを半透膜に置き換えてみると,熱機械効果で生ずる圧力差は浸透圧に似ています。 まとめ 以上のように,超流動4Heは非日常的で興味深い多くの性質を示します。超流動現象は,無数のボース粒子が同じエネルギー基底状態を占有するボース・アインシュタイン凝縮(BEC)と深く関係しています(注5)。そして,電子や核子のようなミクロな粒子の運動を記述する量子力学が,目で見えるほどのマクロなスケールで現れる希有な現象です。1つの原子の中の軌道電子の運動に摩擦があるとは思わないでしょう。しかし,アボガドロ数(= 6.02×1023)ほどの原子からなる液体でそれと同じことが実現するのが超流動現象なのです。4He原子はボース粒子であり,液体は引力のために高い密度をもつので 2.17 K という相対的に“高い”温度で超流動転移します。おかげで,マクロな量子現象を直接目で見ることができるのです。 < 動画製作 > 高吉慎太郎,小田啓太,伊與田英輝,小畑和幸,河合直樹 (注1) 超流動4HeのT = 0での臨界速度は,細孔径が小さいほど大きいという一般的な性質をもちますが,ミクロな表面粗さによって毎秒数cmから数mまでさまざまな値をとります。 (注2) ファン・デル・ワールスの引力ポテンシャルエネルギーは,膜厚を薄くすると(およそその3乗に反比例して)薄くなるほど下がります(絶対値が大きくなる)。一方,重力のポテンシャルエネルギーは,液体の自由表面(液面)からの高さに比例して上がります。ある高さでの膜厚は,液体の温度がどこでも同じならば,この二つの正負のポテンシャルエネルギーが差し引きゼロになる条件で一意に決まり,液面から高いほど薄くなります。このように,平衡状態では,容器中の液体,薄膜,気相という3者の化学ポテンシャルがすべて等しくなっているはずです。
(注3) 超流動4Heには,密度(ρ)の変動が伝搬する通常の疎密波(第1音波)の他に,2成分の比ρS/ρNの変動が伝搬する「第2音波」が存在します。第2音波は,温度波とかエントロピー波と呼ばれるように,ヒーターで励起し温度計で検出することができます。その伝搬速度は第1音波より1桁低い20 m/sくらいです。 (注4) ラムダ点における突沸停止の説明で,超流動相は桁違いに大きな熱伝導度をもつことを書きましたが,これは2流体モデルでは「熱対抗流」の結果として理解できます。液体のある場所に熱が入ると,そこに向かって超流動成分が流れ込み,その熱で常流動成分に姿を変えて元来た経路を逆向きに流れるのが熱対抗流です(正味の液体の流れはゼロ:ρS + ρN = 0)。両成分の間には摩擦がないため,臨界速度を超えない範囲で,これは理想的な熱吸収ができることを意味します(理想的な熱対流)。つまり,超流体の中に温度差をつけたり,大きな熱ゆらぎをもたせることは不可能なのです。 (注5) ボース統計に従う相互作用が無視できる粒子からなる気体(理想ボース気体)は,ある有限温度(TBEC)以下で,マクロな数の粒子が最低エネルギー状態(運動量ゼロ)を占有しはじめ,T = 0ではすべての粒子がその状態を占めます。この現象を「ボース・アインシュタイン凝縮(BEC)」といい,最低エネルギー状態にある粒子のことを「凝縮体」とよびます。これは1925年にアインシュタインが予言した不思議な現象ですが,1938年に見つかった液体4Heの超流動現象は,このBECが初めて,事実上,具現化したものです。ここで“事実上”という理由は,気体と違って液体では原子間相互作用の効果が大きいので,超流動4Heでは,アインシュタインの予言と定量的に少し異なり,絶対零度でも粒子は運動量ゼロのまわりで一定の分布をもち,ゼロ運動量の凝縮体は全粒子数のおよそ10%にとどまるからです。この方が,原子間の強い近距離斥力を効果的に避けて系のエネルギーをより下げることができるからです。そして,その分布をもつ状態(基底状態)こそが2流体モデルにおける超流動成分に当たります。そして,常流動成分の正体は,有限温度で基底状態から熱励起された密度ゆらぎ(フォノンとかロトンとよばれる)であることが,ランダウによって示されています。一方,アインシュタインの予言と定量的にも近いBEC現象は,1995年にレーザー冷却された希薄アルカリ原子気体で発見されました。 |